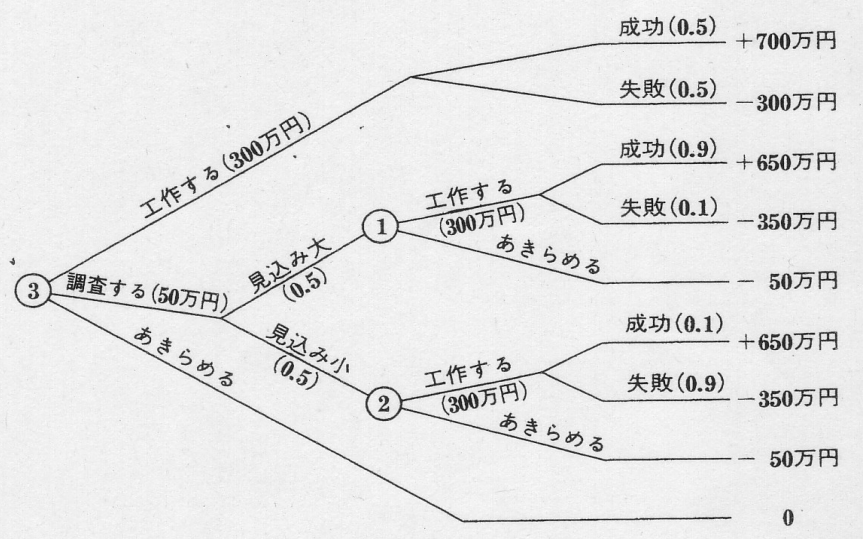
図20.1 ディシジョン・ツゥリー(受注できれば1000万円の意思決定)
過去の実績からある時期の日曜日の弁当の売れ具合(純利益)が下記のように大略 分かっているとする。
| 晴れの場合 | 雨模様の場合 | |
|---|---|---|
| 東京 | 80万円 | 10万円 |
| 横浜 | 70万円 | 30万円 |
| 埼玉 | 40万円 | 40万円 |
前の日に、晴れの確率が40%、雨模様の確率が60%と分かった場合、どの地域 に向けた弁当作りをすれば利益を最大に出来るか?
期待値を比較すると下記のようになる。
| 東京: 80 × 0.4+10 × 0.6=38万円 |
| 横浜: 70 × 0.4+30 × 0.6=46万円 |
| 埼玉: 40 × 0.4+40 × 0.6=40万円 |
図20.1 は、受注できれば“売り上げ1000万円の仕事”の意思決定に関するディ シジョントゥリーである。①先ず受注工作するか、②調査するか、③諦めるか の選択 肢があり、この中から期待値が最大となる選択肢を見つける。
受注できれば利益1000万円の意思決定!(ディシジョン・トゥリー) ●先ず受注工作するか、●調査するか、●諦めるか!!
それぞれの選択肢の期待値を計算すると下記のようになる。
700 × 0.5-300 × 0.5=200万円
650 × 0.9-350 × 0.1=550万円
∴ 550 × 0.5-50 × 0.5=250万円650 × 0.1-350 × 0.9=-250万円
一方②で諦める場合はー50万円 ∴①>②| 晴れの場合 | 雨模様の場合 | |
|---|---|---|
| 東京 | 80万円 | 10万円 |
| 横浜 | 70万円 | 30万円 |
| 埼玉 | 40万円 | 40万円 |
結果: ミニマムである雨模様の場合の10万円、30万円、40万円のうち Max. である40万円を採用。
結果: ex. 晴れに 0.3 を選択(従って雨模様は 1-0.3=0.7)して加算結果の max. を採用すると横浜の 42 万円を採用することになる。
・・・ 期待値はいずれも100万円
↓
多分現生に手を出すはず
| くじ | 当たる確率(%) | 賞金額(万円) |
|---|---|---|
| A | 90 | 100 |
| B | 70 | 300 |
| C | 40 | 600 |
| D | 10 | 1000 |