品質管理には,下記に示すようなさまざまな管理体系がある.
- ① QC (Quality Control)品質管理
顧客の品質要求を満たすため,製品・サービスなどに盛り込む品質システムに基づい た活動である.ボトムアップの小集団活動であるQCサークルとして,多くの製造メー カーで古くから採用されている.
- ②SQC (Statistical Quality Control) 統計的品質管理
統計的手段を用いて品質管理を行う活動である.
- ③TQC (Total Quality Control) 総合品質管理
品質管理を効果的に行うため,市場調査から開発,企画,設計,調達,製造,検査, 販売,サービス,教育などの企業活動全段階にわたって参画して行う活動である.
- ④TQM (Total Quality Management) 総合品質経営管理
品質方針,品質目標・責任を定め,品質計画,品質保証,品質改善などを実施する経 営活動である.
- 品質が経営方針の第一である.
- 高品質を作り込む仕組み作りのスキルが高い.
- 全員参加の品質管理活動がモットーである.製造部門+技術・購買・販売部門の協力 や,QCサークルをフル活用する.
- ツールの開発意欲が高い.統計的品質管理や,“QC七つ道具”などが利用されている.
- ①パレート図
クレームなどを損失金額,原因別など,出現頻度を大きい順に並べるとともに,累 積和を示した図である.重点順位がわかり,何を改善すべきかが一目瞭然となる.
- ②特性要因図(Fish bone)
不良の要因と特性との関連を,系統的に魚の骨のように表した図である.
- ③チェックリストまたはチェックシート
作業手順などを,チェックしながらデータ記録するための表である.
- ④ヒストグラム
特性値のバラツキの程度や,分布の仕方を表す棒状の図である.
- ⑤層別
製造条件や素性が似たものを一まとめにして,条件が違うものと区別してデータを 取ることであり,たとえば機械別,時間別,材料別,人間別といったデータのグループ 分け分析を行う.
- ⑥散布図
二つの特性を横軸と縦軸とし,測定値をプロットして対応する二つの特性の相関を 見るものである.
- ⑦グラフ・管理図
特性値を時系列変動などによる管理をするためのもので,上側管理限界線や下側管 理限界線を有する図である.
この他に,さらに“新QC 七つ道具”というものもある.これは,管理者やスタッフの TQC のために用いられる言語データ的品質管理手法であり,“ QC 七つ道具”と併用さ れる場合が多い.
“新QC七つ道具”は,- ①親和図法
バラバラな情報から問題点を確定させるための手法で,川喜多二郎博士のKJ法で ある.
- ②連関図法
考えられる発生原因が沢山あって,複雑に絡み合っている場合,因果関係を探って いき,最終的に最も影響が大きい要因を決定する手法である.
- ③系統図法(ツリーダイヤグラム)
問題解決という目的に対して,手段や方策をツリー状に展開し,最適手段を系統的 に定める手法である.
- ④マトリックス図法
多くの目的や現象と,多くの手段や要因のそれぞれの対応関係を整理して行列形式 で並べ,相互の関連の程度をたとえば○,△, × などを付けて整理する手法である.
- ⑤アローダイヤグラム法
計画推進のための最適日程管理を行う“PERT手法”のことである.工程順に矢印 を引き,最長の日程経路をクリティカルパスと定めて,この工程を重点的に管理するこ とで,納期に間に合うよう進捗状況を効率よく管理するツールである.
- ⑥PDPC( Process Decision Program Chart )
過程計画決定図と呼ばれ,問題や不測の事態で,日程計画通りに進められなくなった場 合の対応策を検討しておき,それに沿っての行動や,新たな考えを入れようとする手法 である.あらかじめ,起こりうるあらゆるケースを想定しておく“強制連結型PDPC” と,逐次修正しながら目標に向って行く“逐次展開型PDPC”の二種類がある.
- ⑦マトリックスデータ解析法
多数の数値データを整理する方法で,マトリックスに、あとめた多くの数値データ を二次元平面上に展開し,主要な問題や原因をわかりやすく定める手法である.
- 品質の種類とその管理・運用
たとえば「エアコンの品質が良い」ということは,下記のようにそれぞれの段階で 意味が存在するのである.
- 市 場 品 質 :使う人が満足している度合い
- 設 計 品 質 :設計者が決めた仕様、諸量
- 製 造 品 質 :製造者が作るときの良品率,できばえ
- 工 事 品 質 :施工業者が据え付けるときのできばえ
- サービス品質 :故障したときの修理のできばえ(保守・メンテナンス内容とユーザ ー対応)
市場品質を確保・実現するために,適切な設計品質や,製造品質を達成することが 必要になる.消費者の欲求を満足する品質を作り出すための手順が,品質管理といえる
その手順とは,- やり方の標準を決める(Plan)
- 決めた通りに実行する(Do)
- 結果を調べて統計的に異常があるかどうかをみる(Check)・・・異常がなけれ ば標準通りの作業を継続する.
- もし異常があればその原因を調べ,処置を講ずる(Action)
具体的には,たとえば製造業では,
“Plan(設計)⇒Do(製造)⇒Check(販売)⇒Action(調査・サービス)⇒Plan”
のサークルを回す行為となる.品質管理はこの繰り返し作業である. 図8.1は品質の適正水準のイメージを示すものであり,コストと販売価格との関 連を考慮する必要がある.顧客の要求とコストを考慮し,保有する技術手段を駆使して 顧客の満足いく品質設計を行うことが重要である.
品質の設計とは,リサイクル使用対応も含め,環境にも配慮した顧客・消費者の満 足を得ることに尽きる(図 8.2参照).
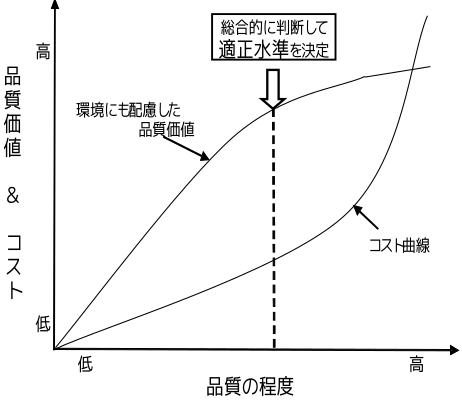
図8.1 品質の適正水準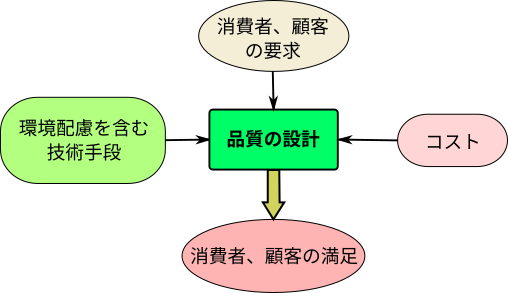
図8.2 品質の設計 - お客様は何に対してお金を払うか
商品の機能・“ハタラキ”を,お客様に約束することが重要である.これはすなわち, 品質を保証することに帰着する.お客様の手元に入いってからの品質(時間的品質)が重要で あり,これにお金を払っているわけで,これが次に述べる“信頼性”である.
8.2 信頼性
8.2.1 信頼性とは
- JISZ 8115による定義
文言による定義は難しいが,要は顧客の信頼を裏切らないことである.
- ①アイテムが与えられた条件のもとで規定の期間中,要求された機能を果たすことができる性質をいう.
- ②アイテムとは,信頼性の対象となるシステム,サブシステム,機器,装置,構成品,部品,素子,要素などの総称をさしている.
- 信頼性保証の必要性
- 故障は,メーカーの保証期間が過ぎてから発生する場合があり,お客様に負担をかけ るとともにメーカーへの信頼感を損なう.
- 故障は,設計要因により発生する場合が多い.
8.2.2 信頼性設計の基本
- バスタブ曲線(故障率曲線)
一般に故障率は図8.3a のように表され,形状がバスタブに似ているところからバス タブ曲線(故障率曲線)と呼ばれている.
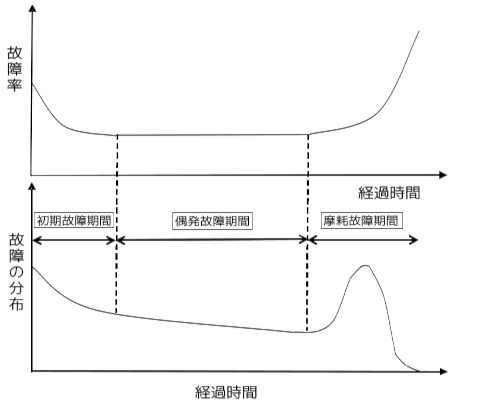
図8.3a バスタブ曲線(故障率曲線)と故障率の分布故障の段階には三種類あることがわかる.信頼性設計では,このバスタブ曲線にお いて次の二点が要求される.
- 偶発故障率λcを下げる.
- 設計寿命を偶発故障期間内に設定する.
図8.3b に示すように,設計寿命は初期故障期間に,余裕期間を差し引いた偶発故 障期間を加えた期間としている.
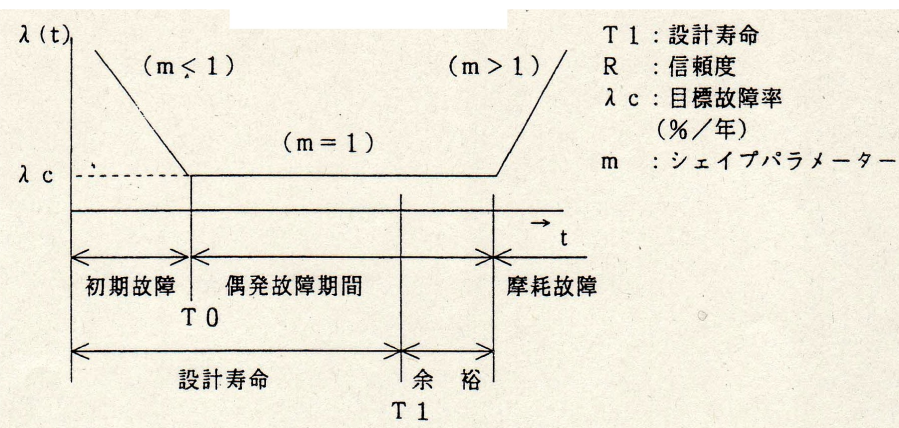
図8.3b バスタブ曲線における設計寿命の範囲 - 信頼性の三大要素
下記のような表示法がある.
- ① 平均故障間隔:一般にMTBF( mean time between failures )と呼ばれた り記述されているもので,故障の少ない性質,すなわち平均寿命を表す.
- ② 平均修復時間:一般にMTTR( mean time to Repair )と呼ばれたり記述されているもので,長持ちする性質を表す.また,MTTF( mean time to failure)ともいう.
- ③ 保全性:一般に Maintainability と呼ばれており,修理コスト,サービス能力を表す.
- MTBF=1/故障率 λc
- MTTR=1/修復率C
- システムの信頼性

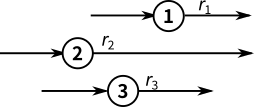
図8.4a 直列システム 図8.4b 並列システム R(t)=r1・r2・r3 ・・・rn
各ユニットの信頼度が同じ場合には,R(t)=rn
となる.したがって各ユニットの信頼度が異なる場合には,最も信頼度の低いユニット が全体システムの信頼性を支配することになる.なお,信頼度と故障確率F (t) との関係は以下の通りである.
R(t) =1-F(t) (故障確率:不信頼度ともいう)
あるいは,F(t) =1-R(t)
で表される.各ユニットもシステム全体も同様である.次に,図 8.4b に示す並列システムの信頼性について考えてみよう.並列の場合,す べてのユニットが故障しない限り,システム全体が故障したことにはならない.したが ってシステム全体の信頼度は,前述の関係を使って,各ユニットの故障率をすべて乗じ たものを,1から差し引いた値になる.
R(t) =1-(1-r1)(1-r2)(1-r3)・・・(1-rδ)
すなわち,R(t) =1-(1-r)δ
となる.ここでδは冗長度ともいえるものであり,信頼度は並列システムの方が高いことが理解されよう.
- ワイブル分析
これは信頼性データの解析に必須のツールである. ワイブル確率紙 と呼ばれる用紙を 利用したデータ分析のことであり,このような用紙が市場に提供されているので,それ に実データをプロットすることで,下記の項目がわかるというものである.
ワイブル確率紙で求めることのできる項目は,①MTBF, ②R (t) , ③F (t) , ④形状パラメータ (shape parameter)“m” ,である.形状パラメータ“ m” については後述する. また,各ユニットを連ねた全体システムについて, - ストレスがかかったとき,最も弱い箇所が壊れる.
- 数が多くなると弱い箇所の含まれる確率は高い.
- 平均寿命の長いものも短いものあるから,ある一定時間までは絶対に壊れないことも
ある.
として,このような条件を満たすものとして,スェーデンの物理学者ワイブルは,三つ
の故障の型を一つの式で以下のように表した.
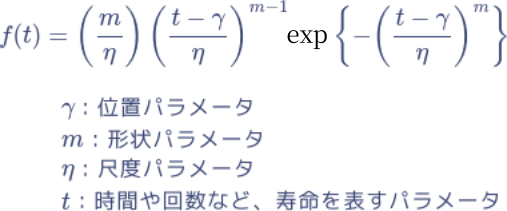
m による故障モードの 判断は以下のように区分される.
- ①m<1 初期故障型
- ②m=1 偶発故障型
- ③m>1 摩耗故障型
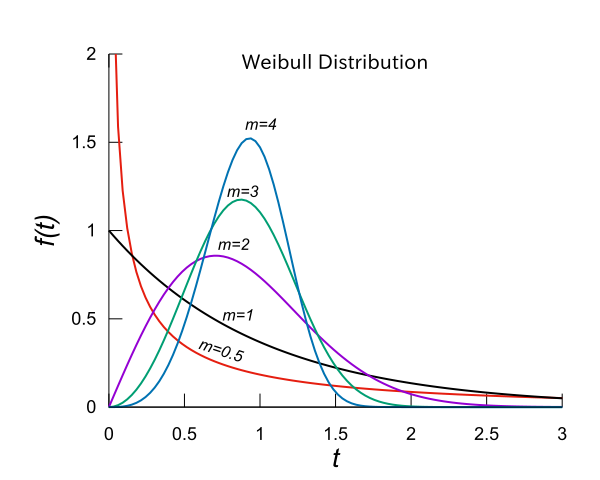
図8.5 “m”によるさまざまな曲線
8.2.3 FTA( Fault Tree Analysis )
考えられる故障原因をツリー状に配置し,下から順に各故障確率を計算して,最終的 に機器やシステム全体の故障確率を求める手法である。
具体的には,どちらか一方に不具合がある場合のみ故障とするORゲート(加算)と, 両方に不具合がある場合のみ故障とするANDゲート(乗算)の組み合わせで構成する.
単純化したわかりやすいイメージを図8.6に示す会議室照明不良の起こる例で 紹介する.
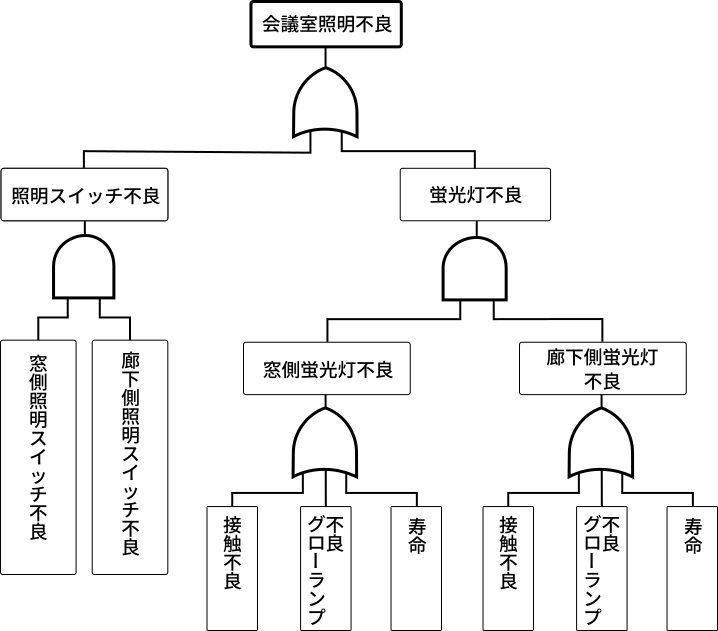
図8.6 FTA手法の一(会議室照明不良の確率をみる)それぞれの不良の起こる確率が算定できれば,最終的に会議室の照明不良の確率が 計算できる.これまでの保守・点検記録や、蛍光灯類の購入実績などから,不良の大ま かな確率は出せる.まったく不明な場合には五分五分にしたり,経験的な数値を採用す ることになる.経験的な数値を採用する場合でも,楽観的な見方と悲観的な見方とで確 率の重み付けが違ってくるのは当然である. 実際の機器やシステムでは,考えうる膨大な故障原因が抽出され,コンピュータに よってツリーを構築して最終的な予想故障確率が求められる.



Copyright 2017 Toshihiko Saito - ①親和図法